What Do I Need to Know for Business Calculus

Bear witness Mobile Detect Show All NotesHibernate All Notes

Mobile Detect

Yous appear to be on a device with a "narrow" screen width (i.east. y'all are probably on a mobile phone). Due to the nature of the mathematics on this site information technology is best views in landscape mode. If your device is not in landscape mode many of the equations volition run off the side of your device (should be able to scroll to run across them) and some of the menu items will be cut off due to the narrow screen width.

Department 4-8 : Optimization

In this department we are going to look at optimization bug. In optimization bug we are looking for the largest value or the smallest value that a office tin can accept. We saw how to solve 1 kind of optimization problem in the Absolute Extrema section where we found the largest and smallest value that a office would take on an interval.

In this section we are going to look at some other blazon of optimization problem. Here we volition exist looking for the largest or smallest value of a role subject field to some kind of constraint. The constraint will exist some status (that can usually exist described by some equation) that must admittedly, positively be truthful no affair what our solution is. On occasion, the constraint volition not be hands described past an equation, but in these problems it will exist like shooting fish in a barrel to bargain with as nosotros'll run into.

This section is generally 1 of the more than difficult for students taking a Calculus course. Ane of the main reasons for this is that a subtle alter of diction can completely modify the trouble. In that location is also the problem of identifying the quantity that we'll be optimizing and the quantity that is the constraint and writing downwards equations for each.

The get-go step in all of these problems should be to very advisedly read the problem. Once yous've done that the adjacent step is to identify the quantity to be optimized and the constraint.

In identifying the constraint remember that the constraint is the quantity that must be true regardless of the solution. In near every one of the bug we'll exist looking at here 1 quantity volition be clearly indicated equally having a stock-still value and so must be the constraint. Once yous've got that identified the quantity to be optimized should exist adequately unproblematic to get. Information technology is still easy to misfile the 2 if you only skim the problem so make sure yous advisedly read the trouble first!

Let's offset the section off with a simple problem to illustrate the kinds of problems we will be dealing with here.

Case 1 We need to enclose a rectangular field with a contend. We take 500 anxiety of fencing fabric and a building is on ane side of the field and then won't need any fencing. Determine the dimensions of the field that volition enclose the largest area.

Show Solution

In all of these problems we volition have two functions. The offset is the function that we are actually trying to optimize and the 2nd will be the constraint. Sketching the situation will oftentimes help us to arrive at these equations and then let's do that.

In this trouble we want to maximize the surface area of a field and we know that will use 500 ft of fencing cloth. So, the area will be the function we are trying to optimize and the amount of fencing is the constraint. The ii equations for these are,

\[\begin{marshal*}{\mbox{Maximize : }} & A = xy\\ {\mbox{Constraint : }} & 500 = 10 + 2y\end{align*}\]

Okay, we know how to find the largest or smallest value of a function provided it's only got a single variable. The area function (as well every bit the constraint) has two variables in it and so what we know about finding absolute extrema won't piece of work. Nonetheless, if nosotros solve the constraint for i of the ii variables nosotros tin can substitute this into the area and we will then have a function of a single variable.

So, let'due south solve the constraint for \(10\). Note that nosotros could have just as easily solved for \(y\) but that would have led to fractions then, in this case, solving for \(x\) will probably exist all-time.

\[x = 500 - 2y\]

Substituting this into the expanse part gives a function of \(y\).

\[A\left( y \right) = \left( {500 - 2y} \right)y = 500y - two{y^2}\]

Now we want to find the largest value this will have on the interval \(\left[ {0,250} \right]\). The limits in this interval corresponds to taking \(y = 0\) (i.e. no sides to the fence) and \(y = 250\) (i.due east. but 2 sides and no width, likewise if in that location are two sides each must exist 250 ft to apply the whole 500ft).

Note that the endpoints of the interval won't make whatever sense from a physical standpoint if nosotros really want to enclose some surface area considering they would both give zippo area. They practise, nevertheless, give us a set of limits on \(y\) and so the Extreme Value Theorem tells us that we volition take a maximum value of the expanse somewhere betwixt the two endpoints. Having these limits will also mean that we tin can use the process we discussed in the Finding Absolute Extrema section earlier in the chapter to find the maximum value of the area.

Then, remember that the maximum value of a continuous office (which we've got hither) on a closed interval (which we also accept here) will occur at critical points and/or end points. As we've already pointed out the terminate points in this example volition requite zero area and then don't make any sense. That means our but option volition exist the disquisitional points.

And so, allow's get the derivative and find the critical points.

\[A'\left( y \correct) = 500 - 4y\]

Setting this equal to cipher and solving gives a lone disquisitional point of \(y = 125\). Plugging this into the area gives an area of \(A\left( {125} \right) = 31250\,{\mbox{f}}{{\mbox{t}}^2}\). And then according to the method from Absolute Extrema department this must be the largest possible area, since the area at either endpoint is zero.

Finally, let'south not forget to get the value of \(ten\) and so nosotros'll have the dimensions since this is what the problem statement asked for. We can get the \(x\) past plugging in our \(y\) into the constraint.

\[x = 500 - 2\left( {125} \right) = 250\]

The dimensions of the field that will give the largest area, subject to the fact that we used exactly 500 ft of fencing material, are 250 x 125.

Don't forget to really read the problem and give the answer that was asked for. These types of problems can take a fair corporeality of time/effort to solve and information technology's non hard to sometimes forget what the problem was actually asking for.

In the previous problem nosotros used the method from the Finding Accented Extrema department to find the maximum value of the office we wanted to optimize. However, as we'll see in later examples it will non ever be like shooting fish in a barrel to find endpoints. Likewise, even if we can find the endpoints we will run into that sometimes dealing with the endpoints may not be easy either. Not only that, just this method requires that the part we're optimizing exist continuous on the interval we're looking at, including the endpoints, and that may not always exist the case.

And then, before proceeding with any more examples let's spend a trivial fourth dimension discussing some methods for determining if our solution is in fact the absolute minimum/maximum value that we're looking for. In some examples all of these will piece of work while in others one or more than won't be all that useful. Withal, we will e'er need to employ some method for making sure that our reply is in fact that optimal value that we're after.

Method 1 : Utilise the method used in Finding Absolute Extrema.

This is the method used in the offset example above. Remember that in order to utilise this method the interval of possible values of the independent variable in the role we are optimizing, let'due south call it \(I\), must have finite endpoints. Also, the function nosotros're optimizing (in one case it's down to a single variable) must be continuous on \(I\), including the endpoints. If these weather condition are met so we know that the optimal value, either the maximum or minimum depending on the problem, will occur at either the endpoints of the range or at a critical point that is inside the range of possible solutions.

At that place are two main issues that will often prevent this method from being used however. Starting time, not every trouble will actually have a range of possible solutions that have finite endpoints at both ends. We'll meet at least ane case of this as we work through the remaining examples. Too, many of the functions nosotros'll be optimizing will not be continuous once nosotros reduce them down to a single variable and this will prevent us from using this method.

Method 2 : Use a variant of the First Derivative Test.

In this method nosotros too will need an interval of possible values of the independent variable in the function we are optimizing, \(I\). However, in this case, unlike the previous method the endpoints do not need to be finite. Too, we will need to require that the function be continuous on the interior of the interval \(I\) and we will only need the function to be continuous at the end points if the endpoint is finite and the function actually exists at the endpoint. Nosotros'll run across several problems where the role we're optimizing doesn't actually be at one of the endpoints. This volition not prevent this method from being used.

Let's suppose that \(x = c\) is a critical point of the part we're trying to optimize, \(f\left( x \right)\). We already know from the Outset Derivative Test that if \(f'\left( 10 \correct) > 0\) immediately to the left of \(ten = c\) (i.e. the office is increasing immediately to the left) and if \(f'\left( ten \right) < 0\) immediately to the right of \(10 = c\)(i.due east. the office is decreasing immediately to the correct) then \(10 = c\) will be a relative maximum for \(f\left( x \right)\).

Now, this does not mean that the absolute maximum of \(f\left( x \correct)\) will occur at \(x = c\). Still, suppose that nosotros knew a little scrap more information. Suppose that in fact we knew that \(f'\left( 10 \correct) > 0\) for all \(x\) in \(I\) such that \(ten < c\). Besides, suppose that nosotros knew that \(f'\left( 10 \right) < 0\) for all \(10\) in \(I\) such that \(10 > c\). In this case nosotros know that to the left of \(10 = c\), provided we stay in \(I\) of class, the function is always increasing and to the correct of \(x = c\), again staying in \(I\), nosotros are always decreasing. In this case nosotros can say that the absolute maximum of \(f\left( x \right)\) in \(I\) will occur at \(10 = c\).

Similarly, if we know that to the left of \(10 = c\) the function is always decreasing and to the right of \(x = c\) the function is always increasing then the absolute minimum of \(f\left( x \correct)\) in \(I\) will occur at \(x = c\).

Before we requite a summary of this method let's discuss the continuity requirement a niggling. Nowhere in the above discussion did the continuity requirement apparently come into play. We crave that the function we're optimizing to be continuous in \(I\) to prevent the following situation.

In this case, a relative maximum of the office conspicuously occurs at \(ten = c\). Also, the function is e'er decreasing to the correct and is always increasing to the left. However, because of the aperture at \(x = d\), we tin clearly run across that \(f\left( d \right) > f\left( c \correct)\) and so the absolute maximum of the function does not occur at \(x = c\). Had the discontinuity at \(x = d\) non been there this would not have happened and the absolute maximum would have occurred at \(x = c\).

Hither is a summary of this method.

Commencement Derivative Test for Accented Extrema

Allow \(I\) be the interval of all possible values of \(x\) in \(f\left( x \right)\), the function we want to optimize, and further suppose that \(f\left( 10 \right)\) is continuous on \(I\) , except mayhap at the endpoints. Finally suppose that \(x = c\) is a disquisitional point of \(f\left( x \right)\) and that \(c\) is in the interval \(I\). If nosotros restrict \(x\) to values from \(I\) (i.eastward. nosotros but consider possible optimal values of the function) then,

1. If \(f'\left( ten \right) > 0\) for all \(ten < c\) and if \(f'\left( x \right) < 0\) for all \(x > c\) then \(f\left( c \correct)\) will be the accented maximum value of \(f\left( x \right)\) on the interval \(I\).
2. If \(f'\left( x \correct) < 0\) for all \(ten < c\) and if \(f'\left( 10 \correct) > 0\) for all \(x > c\) then \(f\left( c \correct)\) volition be the absolute minimum value of \(f\left( x \right)\) on the interval \(I\).

Method 3 : Use the second derivative.

There are actually two ways to utilize the 2d derivative to help the states identify the optimal value of a function and both use the Second Derivative Exam to one extent or another.

The showtime way to use the second derivative doesn't actually assistance the states to place the optimal value. What it does do is allow u.s. to potentially exclude values and knowing this can simplify our work somewhat so is not a bad thing to exercise.

Suppose that nosotros are looking for the absolute maximum of a function and after finding the disquisitional points nosotros find that we have multiple critical points. Permit'southward as well suppose that we run all of them through the second derivative examination and make up one's mind that some of them are in fact relative minimums of the part. Since we are after the absolute maximum we know that a maximum (of any kind) can't occur at relative minimums and so we immediately know that we can exclude these points from further consideration. We could do a similar cheque if nosotros were looking for the absolute minimum. Doing this may not seem similar all that great of a thing to do, simply it tin, on occasion, lead to a nice reduction in the corporeality of work that nosotros need to do in subsequently steps.

The second way of using the second derivative to identify the optimal value of a role is in fact very similar to the second method in a higher place. In fact, we volition have the same requirements for this method equally nosotros did in that method. We need an interval of possible values of the independent variable in part we are optimizing, phone call it \(I\) equally earlier, and the endpoint(s) may or may non exist finite. Nosotros'll also need to require that the function, \(f\left( x \correct)\) be continuous everywhere in \(I\) except perhaps at the endpoints as to a higher place.

Now, suppose that \(x = c\) is a disquisitional point and that \(f''\left( c \right) > 0\). The 2nd derivative test tells the states that \(x = c\) must be a relative minimum of the function. Suppose withal that we also knew that \(f''\left( x \right) > 0\) for all \(x\) in \(I\). In this case nosotros would know that the office was concave upwardly in all of \(I\) and that would in turn mean that the absolute minimum of \(f\left( 10 \right)\) in \(I\) would in fact have to be at \(x = c\).

Likewise, if \(x = c\) is a disquisitional point and \(f''\left( x \right) < 0\) for all \(x\) in \(I\) then nosotros would know that the function was concave down in \(I\) and that the absolute maximum of \(f\left( ten \correct)\) in \(I\) would accept to be at \(x = c\).

Here is a summary of this method.

Second Derivative Test for Absolute Extrema

Let \(I\) exist the interval of all possible values of \(x\) in \(f\left( x \right)\), the role nosotros desire to optimize, and suppose that \(f\left( x \right)\) is continuous on \(I\) , except perchance at the endpoints. Finally suppose that \(x = c\) is a critical point of \(f\left( x \right)\) and that \(c\) is in the interval \(I\). Then,

1. If \(f''\left( 10 \right) > 0\) for all \(x\) in \(I\) then \(f\left( c \correct)\) will exist the absolute minimum value of \(f\left( x \correct)\) on the interval \(I\).
2. If \(f''\left( 10 \right) < 0\) for all \(10\) in \(I\) then \(f\left( c \right)\) will be the absolute maximum value of \(f\left( x \right)\) on the interval \(I\).

As we work examples over the side by side two sections we will apply each of these methods as needed in the examples. In some cases, the method we use will be the merely method we could use, in others it will exist the easiest method to use and in others it will simply be the method we chose to employ for that instance. It is of import to realize that we won't be able to use each of the methods for every case. With some examples i method will be easiest to use or may be the just method that can be used, notwithstanding, each of the methods described above will exist used at least a couple of times through out all of the examples.

It is too important to be aware that some bug don't allow any of the methods discussed above to be used exactly equally outlined above. We may need to modify one of them or use a combination of them to fully piece of work the problem. There is an instance in the next section where none of the methods in a higher place work hands, although nosotros exercise too present an culling solution method in which nosotros can use at least one of the methods discussed above.

Next, the vast majority of the examples worked over the course of the next section volition only have a single critical indicate. Issues with more one critical bespeak are often difficult to know which critical point(southward) requite the optimal value. There are a couple of examples in the next 2 sections with more than one disquisitional bespeak including ane in the next section mentioned above in which none of the methods discussed higher up easily work. In that example you can see some of the ideas you might demand to exercise in society to observe the optimal value.

Finally, in all of the methods in a higher place we referenced an interval \(I\). This was done to make the discussion a piffling easier. However, in all of the examples over the next two sections we will never explicitly say "this is the interval \(I\)". Just remember that the interval \(I\) is only the largest interval of possible values of the contained variable in the function we are optimizing.

Okay, let's work some more examples.

Case ii We want to construct a box whose base length is 3 times the base width. The material used to build the height and bottom cost $10/ft² and the material used to build the sides price $six/ftⁱⁱ. If the box must have a book of 50ftⁱⁱⁱ decide the dimensions that will minimize the price to build the box.

Show Solution

Offset, a quick figure (probably not to scale…).

We want to minimize the cost of the materials subject to the constraint that the book must exist 50ft³. Note as well that the cost for each side is but the area of that side times the appropriate cost.

The two functions we'll be working with hither this time are,

\[\begin{align*}{\mbox{Minimize : }} & C = 10\left( {2lw} \right) + half-dozen\left( {2wh + 2lh} \right)\, = lx{west^two} + 48wh\\ {\mbox{Constraint :}}& 50 = lwh = 3{w^2}h\end{align*}\]

Every bit with the first example, we volition solve the constraint for ane of the variables and plug this into the price. It will definitely be easier to solve the constraint for \(h\) then let's practise that.

\[h = \frac{{50}}{{3{w^ii}}}\]

Plugging this into the cost gives,

\[C\left( due west \correct) = 60{west^2} + 48w\left( {\frac{{50}}{{3{w^two}}}} \right) = 60{due west^ii} + \frac{{800}}{w}\]

At present, let'south become the first and second (nosotros'll exist needing this afterward…) derivatives,

\[C'\left( due west \right) = 120w - 800{w^{ - 2}} = \frac{{120{due west^3} - 800}}{{{west^two}}}\hspace{0.25in}\hspace{0.25in}C''\left( west \right) = 120 + 1600{westward^{ - iii}}\]

Now we need the critical point(s) for the cost function. First, notice that \(w = 0\) is not a critical indicate. Clearly the derivative does non exist at \(w = 0\) but then neither does the function and retrieve that values of \(w\) will only be critical points if the function also exists at that point. Notation that there is as well a physical reason to avoid \(w = 0\). We are amalgam a box and it would make no sense to accept a zero width of the box.

So it looks similar the only disquisitional point will come from determining where the numerator is zilch.

\[120{west^3} - 800 = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,w = \sqrt[3]{{\frac{{800}}{{120}}}} = \sqrt[3]{{\frac{{twenty}}{three}}} = 1.8821\]

So, we've got a single critical indicate and we now have to verify that this is in fact the value that will give the absolute minimum price.

In this case we can't use Method 1 from above. Offset, the function is not continuous at one of the endpoints, \(w = 0\), of our interval of possible values, i.e. \(w > 0\). Secondly, at that place is no theoretical upper limit to the width that will give a box with volume of 50 ftⁱⁱⁱ. If \(westward\) is very large and then we would just need to make \(h\) very pocket-sized.

The second method listed above would work here, but that's going to involve some calculations, non difficult calculations, but more than work nonetheless.

The tertiary method even so, will work apace and simply here. Outset, nosotros know that whatsoever the value of \(w\) that we go it will have to be positive and we tin see 2d derivative above that provided \(west > 0\) nosotros will take \(C''\left( west \correct) > 0\) then in the interval of possible optimal values the cost function will always be concave up and and so \(west = 1.8821\) must give the absolute minimum cost.

All we need to exercise now is to find the remaining dimensions.

\[\begin{align*}w & = one.8821\\ l & = 3w = 3\left( {1.8821} \right) = v.6463\\ h & = \frac{{l}}{{3{w^two}}} = \frac{{50}}{{3{{\left( {1.8821} \right)}^two}}} = 4.7050\end{marshal*}\]

Also, even though it was non asked for, the minimum cost is : \(C\left( {1.8821} \right) = \$ 637.60\).

Instance 3 We desire to construct a box with a square base and we only accept 10 chiliadⁱⁱ of textile to use in structure of the box. Assuming that all the fabric is used in the structure procedure make up one's mind the maximum volume that the box tin can accept.

Show Solution

This example is in many ways the verbal contrary of the previous case. In this case nosotros want to optimize the volume and the constraint this time is the amount of material used. We don't accept a toll here, merely if y'all think about it the cost is nothing more than than the amount of cloth used times a price and and so the corporeality of material and cost are pretty much tied together. If you can do 1 yous can practise the other as well. Note also that the corporeality of material used is really just the surface area of the box.

Every bit always, let'southward start off with a quick sketch of the box.

Now, as mentioned above we want to maximize the volume and the amount of material is the constraint so hither are the equations we'll need.

\[\brainstorm{align*}{\mbox{Maximize : }} & V = lwh = {w^2}h\\ {\mbox{Constraint :}} & 10 = 2lw + 2wh + 2lh\, = 2{w^2} + 4wh\end{align*}\]

Nosotros'll solve the constraint for \(h\) and plug this into the equation for the volume.

\[h = \frac{{ten - ii{w^two}}}{{4w}} = \frac{{v - {west^2}}}{{2w}}\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,\,\,\,\,Five\left( w \correct) = {w^2}\left( {\frac{{5 - {west^2}}}{{2w}}} \right) = \frac{1}{2}\left( {5w - {w^3}} \right)\]

Here are the kickoff and second derivatives of the volume function.

\[V'\left( west \correct) = {{1 \over 2}}\left( {five - 3{w^two}} \right)\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}V''\left( w \right) = - 3w\]

Note every bit well here that provided \(w > 0\), which from a physical standpoint we know must exist true for the width of the box, then the volume function volition be concave downward and so if we get a single critical point so we know that it will have to be the value that gives the absolute maximum.

Setting the kickoff derivative equal to nix and solving gives us the two critical points,

\[w = \pm \,\sqrt {\frac{5}{3}} = \pm \,1.2910\]

In this case we can exclude the negative disquisitional point since we are dealing with a length of a box and we know that these must be positive. Practice not withal become into the habit of just excluding any negative disquisitional point. There are problems where negative critical points are perfectly valid possible solutions.

Now, as noted above we got a single disquisitional point, 1.2910, and then this must be the value that gives the maximum volume and since the maximum volume is all that was asked for in the trouble argument the respond is and so : \[V\left( {1.2910} \correct) = 2.1517\,{{\mbox{m}}^3}\].

Notation that we could too have noted hither that if \(0 < west < 1.2910\) then \(5'\left( due west \right) > 0\) (using a test point nosotros have \(5'\left( 1 \right) = 1 > 0\)) and likewise if \(west > 1.2910\) then \(Five'\left( w \right) < 0\) (using a exam point we have \(Five'\left( 2 \right) = - {\frac{7}{two}} < 0\)) and and so if we are to the left of the disquisitional point the volume is always increasing and if we are to the correct of the critical point the volume is e'er decreasing and then by the Method 2 to a higher place we tin likewise come across that the single critical signal must give the absolute maximum of the book.

Finally, even though these weren't asked for here are the dimension of the box that gives the maximum volume.

\[l = due west = ane.2910\hspace{1.0in}h = \frac{{five - {{1.2910}^2}}}{{two\left( {i.2910} \right)}} = 1.2910\]

Then, it looks like in this example we actually have a perfect cube.

In the last two examples we've seen that many of these optimization problems can be done in both directions and so to speak. In both examples nosotros take essentially the same two equations: volume and surface area. Even so, in Case 2 the volume was the constraint and the cost (which is directly related to the surface expanse) was the function we were trying to optimize. In Case 3, on the other hand, we were trying to optimize the volume and the surface surface area was the constraint.

It is important to not get then locked into one way of doing these problems that we can't do information technology in the opposite direction as needed likewise. This is one of the more than common mistakes that students make with these kinds of problems. They see one trouble and so endeavor to make every other problem that seems to be the aforementioned conform to that ane solution even if the problem needs to be worked differently. Keep an open mind with these problems and make sure that yous sympathize what is being optimized and what the constraint is before you spring into the solution.

Likewise, as seen in the last example we used ii different methods of verifying that we did get the optimal value. Exercise not go too locked into one method of doing this verification that you forget about the other methods.

Permit'southward piece of work some another example that this time doesn't involve a rectangle or box.

Example 4 A manufacturer needs to brand a cylindrical can that will hold i.5 liters of liquid. Determine the dimensions of the can that volition minimize the amount of material used in its construction.

Show Solution

Before starting the solution let's get-go accost the fact that we are using liters for volume. Because we desire length measurements for the radius and meridian nosotros'll besides need the volume to in terms of a length measurement. Nosotros tin can easily do this using the fact that 1 Liter = 1000 cm³ and so we tin catechumen 1.5 liters into 1500 cm^three. This will in turn requite a radius and height in terms of centimeters.

In this trouble the constraint is the book and nosotros desire to minimize the amount of cloth used. This means that what nosotros desire to minimize is the expanse of the can and we'll demand to include both the walls of the can as well as the pinnacle and lesser "caps". Here is a quick sketch to get us started off.

Nosotros'll need the surface expanse of this can and that will be the surface area of the walls of the can (which is actually but a cylinder) and the surface area of the superlative and bottom caps (which are just disks, and don't forget that at that place are two of them).

Note that if you recollect of a cylinder of height \(h\) and radius \(r\) equally only a bunch of disks/circles of radius \(r\) stacked on acme of each other the equations for the surface area and book are pretty uncomplicated to remember. The volume is but the area of each of the disks times the superlative. Similarly, the surface surface area of the walls of the cylinder is just the circumference of each circumvolve times the tiptop. We besides can't forget to add in the expanse of the ii caps, \(\pi {r^2}\), to the total surface area.

Then, the equation for the volume and surface area of the walls of a cylinder are then,

\[Five = \left( {\pi {r^2}} \correct)\left( h \correct) = \pi {r^ii}h\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}A = \left( {two\pi r} \right)\left( h \right) = two\pi rh\]

Adding the surface area of the caps of the cylinder to the surface expanse the equations that we'll need for this problem are,

\[\brainstorm{align*}{\mbox{Minimize : }} & A = 2\pi rh + 2\pi {r^ii}\\ {\mbox{Constraint :}} & 1500 = \pi {r^two}h\end{align*}\]

In this case it looks like our best option is to solve the constraint for \(h\) and plug this into the area function.

\[h = \frac{{1500}}{{\pi {r^2}}}\hspace{0.25in} \Rightarrow \hspace{0.25in}A\left( r \correct) = 2\pi r\left( {\frac{{1500}}{{\pi {r^two}}}} \right) + 2\pi {r^2} = ii\pi {r^two} + \frac{{3000}}{r}\]

Notice that this formula will only make sense from a concrete standpoint if \(r > 0\) which is a good affair equally it is not defined at \(r = 0\).

Next, let's go the showtime derivative.

\[A'\left( r \correct) = iv\pi r - \frac{{3000}}{{{r^2}}} = \frac{{4\pi {r^iii} - 3000}}{{{r^two}}}\]

From this we can see that we take ane disquisitional points : \(r = \sqrt[3]{\frac{750}{\pi}} = six.2035\)(where the derivative is naught). Notation that \(r = 0\) is not a critical point because the expanse part does non exist there, which makes sense from a physical standpoint likewise given that we know that \(r\) must exist positive in lodge to really accept a tin.

So, we only take a unmarried disquisitional point to deal with here and notice that half-dozen.2035 is the just value for which the derivative will exist zero and hence the only place (with \(r > 0\) of course) that the derivative may modify sign. Information technology'south non difficult, using exam points, to check that if \(0 < r < 6.2035\) then \(A'\left( r \correct) < 0\) and likewise if \(r > 6.2035\) then \(A'\left( r \right) > 0\). The variant of the Showtime Derivative Test above then tells u.s.a. that the absolute minimum value of the area (for \(r > 0\)) must occur at \[r = 6.2035\].

All we need to do this is make up one's mind top of the tin and nosotros'll exist done.

\[h = \frac{{1500}}{{\pi {{\left( {half-dozen.2035} \correct)}^2}}} = 12.4070\]

Therefore, if the manufacturer makes the tin can with a radius of half dozen.2035 cm and a height of 12.4070 cm the least amount of textile will exist used to make the tin can.

As an interesting side problem and extension to the to a higher place example you might desire to show that for a given volume, \(L\), the minimum textile will exist used if \(h = 2r\) regardless of the volume of the tin can.

In the examples to this indicate we've put in quite a chip of discussion in the solution. In the remaining bug we won't be putting in quite every bit much discussion and exit it to yous to fill in any missing details.

Example 5 We take a piece of cardboard that is 14 inches by 10 inches and we're going to cut out the corners as shown below and fold upward the sides to form a box, also shown below. Determine the height of the box that will requite a maximum volume.

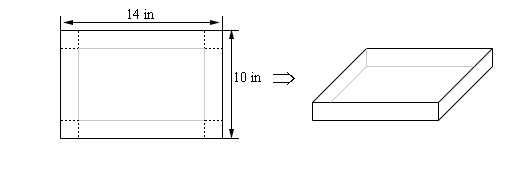
Show Solution

Allow'south let the height of the box exist \(h\). So, the width/length of the corners being cut out is besides \(h\) so the vertical side will take a "new" height of \(ten - 2h\) and the horizontal side will have a "new" width of \(14 - 2h\). Here is a sketch with all this data put in,

In this example, for the first time, we've meet a problem where the constraint doesn't really take an equation. The constraint is simply the size of the piece of paper-thin and has already been factored into the figure above. This will happen on occasion so don't go excited about it when it does. This just means that we take one less equation to worry about. In this example we desire to maximize the volume. Here is the volume, in terms of \(h\) and its first derivative.

\[V\left( h \correct) = h\left( {14 - 2h} \right)\left( {10 - 2h} \right) = 140h - 48{h^2} + 4{h^3}\hspace{0.25in}\hspace{0.25in}5'\left( h \correct) = 140 - 96h + 12{h^2}\]

Setting the first derivative equal to nix and solving gives the following ii critical points,

\[h = \frac{{12 \pm \sqrt {39} }}{three} = ane.9183,\,\,\,\,half-dozen.0817\]

We at present have an credible trouble. We have two disquisitional points and we'll need to determine which i is the value we need. The fact that nosotros have two critical points means that neither the beginning derivative test or the second derivative exam can be used here as they both require a single critical indicate. This isn't a existent problem withal. Become back to the figure at the starting time of the solution and notice that nosotros can quite hands find limits on \(h\). The smallest \(h\) tin be is \(h = 0\) fifty-fifty though this doesn't brand much sense as we won't get a box in this case. Also, from the 10 inch side we can see that the largest \(h\) can exist is \(h = 5\) although again, this doesn't brand much sense physically.

So, knowing that whatever \(h\) is information technology must be in the range \(0 \le h \le 5\) we tin see that the second critical point is outside this range and then the merely critical point that nosotros need to worry about is i.9183.

Finally, since the volume is defined and continuous on \(0 \le h \le 5\) all nosotros need to practice is plug in the critical points and endpoints into the volume to decide which gives the largest volume. Here are those function evaluations.

\[V\left( 0 \correct) = 0\hspace{0.25in}\hspace{0.25in}Five\left( {ane.9183} \right) = 120.1644\hspace{0.25in}\hspace{0.25in}V\left( 5 \right) = 0\]

Then, if we take \(h = ane.9183\) we get a maximum volume.

Case 6 A printer needs to make a poster that will accept a total area of 200 in² and volition take 1 inch margins on the sides, a 2 inch margin on the top and a 1.v inch margin on the bottom as shown beneath. What dimensions volition give the largest printed surface area?

Bear witness Solution

This problem is a little different from the previous problems. Both the constraint and the office we are going to optimize are areas. The constraint is that the overall surface area of the poster must be 200 in² while we desire to optimize the printed area (i.due east. the area of the affiche with the margins taken out).

Allow's define the height of the affiche to be \(h\) and the width of the poster to exist \(west\). Here is a new sketch of the poster and we can see that once we've taken the margins into account the width of the printed area is \(w - 2\) and the elevation of the printer area is \(h - three.5\).

Here are the equations that we'll exist working with.

\[\brainstorm{align*}{\mbox{Maximize : }} & A = \left( {westward - 2} \right)\left( {h - 3.5} \right)\\ {\mbox{Constraint :}} & 200 = wh\finish{align*}\]

Solving the constraint for \(h\) and plugging into the equation for the printed expanse gives,

\[A\left( w \right) = \left( {due west - 2} \right)\left( {\frac{{200}}{w} - iii.5} \right) = 207 - 3.5w - \frac{{400}}{w}\]

The offset and second derivatives are,

\[A'\left( w \right) = - iii.5 + \frac{{400}}{{{w^ii}}} = \frac{{400 - three.v{west^2}}}{{{w^2}}}\hspace{0.25in}\hspace{0.25in}A''\left( w \right) = - \frac{{800}}{{{w^3}}}\]

From the first derivative we take the following two critical points (\(w = 0\) is non a disquisitional betoken because the expanse function does not be in that location).

\[due west = \pm \,\sqrt {\frac{400}{iii.five}} = \pm \,10.6904\]

However, since we're dealing with the dimensions of a piece of paper nosotros know that nosotros must have \(w > 0\) so only 10.6904 volition make sense.

Also notice that provided \(w > 0\) the second derivative will e'er exist negative and then in the range of possible optimal values of the width the area function is always concave downward and so we know that the maximum printed area will be at \(w = 10.6904\,\,{\mbox{inches}}\).

The summit of the paper that gives the maximum printed area is then,

\[h = \frac{{200}}{{10.6904}} = 18.7084\,\,{\mbox{inches}}\]

We've worked quite a few examples to this point and we take quite a few more to piece of work. Still, this department has gotten quite lengthy then let'south go along our examples in the next section. This is beingness washed mostly because these notes are besides existence presented on the web and this volition help to proceed the load times on the pages down somewhat.

mayyoune1981.blogspot.com

Source: https://tutorial.math.lamar.edu/Classes/CalcI/Optimization.aspx